【フェルミ推定】日本の電柱の本数は？MECEのセンスを高めて論理力を鍛えよう

論理的思考力は、仕事や勉強だけでなく、遊びでも鍛えることが出来ます。

どうせ鍛えるなら、楽しみながら鍛えたいものですよね？

というわけで、今回はMECEの切り口センスを高める「フェルミ推定」を用いた論理トレーニングをご紹介したいと思います。具体例としては、日本の電柱の総本数の計算を取り上げています。

フェルミ推定とは？

フェルミ推定とは、実際に調べることが難しいものをいくつかの要素に分解して論理的に推定する手法のことを指します。名前は物理学者のエンリコ・フェルミに由来するそうです。

時には、order estimation（桁数推定）と呼ばれる場合もあります。

そして、フェルミ推定の核である要素分解が、MECEの切り口センスを高めてくれます。

というわけで、実際の問題を解きつつ考えていきたいと思います。

「日本全国にある電柱の数はいくつあるのか」という有名問題について考えたいと思います。

ここから解答となりますので、皆さんも一度立ち止まって考えてみてください。

まずは、電柱の特徴について考えてみましょう。そうすると、次のようなことが考えられます。

以上の項目は、多くの人が妥当と考える電柱の特徴だと思います。

このように、切り分ける対象の特徴を考えると、効果のあるMECEを行えるようになります。

1番の特徴を利用すると、次のような計算式で電柱の本数を考えることが出来ます。

電柱の本数＝道路の総延長×電柱の平均間隔

しかし、この式を活用するためには、道路の総延長距離を計算しなければなりません。

総延長距離の計算は、次の式で計算可能です。

総延長距離＝（平地の面積×道路の割合（平地）＋山地の面積×道路の割合（山地））/道路幅

日本の面積は38万km2で、平地は3割、山地は7割を占めます。あとは、道路の割合と幅の仮定です。この部分については後ほど…

このように、概算したい対象をMECEを意識して切り分けて、既知の数字や概算可能な数字に置き換えます。これが、フェルミ推定の核心部分であり、この過程を考えることが論理トレーニングとなります。

後は、分割した要素に数字を当てはめるだけです。

ここでは、電柱間隔を10m、平地の道路割合を1/10～1/100、山地の道路割合は平地と比較して無視できるほど小さいとします。そして、道路幅は5mを仮定します。

計算結果は次のエクセル表をご覧ください。

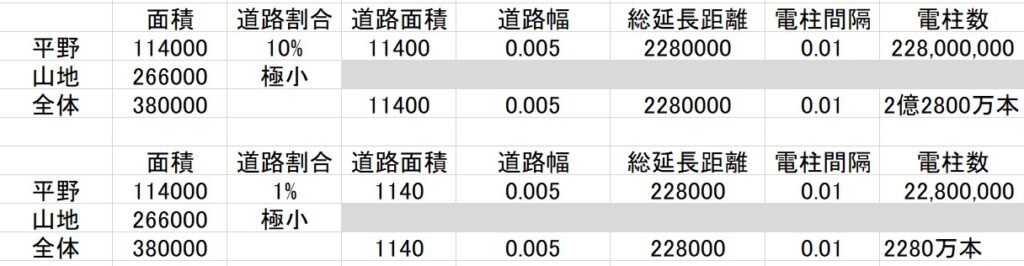
総延長距離は22.8万km～228万kmとなっていますね。実際の総延長距離は127万キロなので、予測に近い値となっています。

そして、電柱の本数は、2億2800万～2800万本となります。実際の電柱本数は約3500万本なので、こちらも予測に近い値になっています。

割とざっくりとした数値を代入して計算していますが、実際の数値とも近い値が出ていますね。

このように、複雑な対象を要素分解して、既知の数字と概算可能な数字に置き換えることで、対象の桁数を予測できます。

このフェルミ推定によって、対象の特徴を理解し、それに基づいてMECEする能力が身に付きます。皆さんも身の回りにあるものをフェルミ推定して頭の体操をしてみてはいかがでしょうか？

フェルミ推定をすることによって、次の三つの能力を身に着けることが出来ます。

この能力を鍛えることで、新たな仕事にも柔軟に対応できるのはもちろんのこと、人の報告を聞いて的確な質問・アドバイスができるようになります。

そのため、外資系企業の面接ではフェルミ推定の問題が出題されることもあります。

ですから、プレイヤーの方はもちろんのこと、マネジメント職の方も息抜きにフェルミ推定をしてみてはいかがでしょうか？